One pillar of the modern world was the project to transform science from a discipline for contemplating nature into a tool for mastering it. Queen among the new sciences was mathematical physics, made possible by a corresponding transformation of mathematics. Ancient mathematicians, said René Descartes, had misunderstood their subject. They offered a procession of dazzling spectacles, but mathematics properly understood is not the presentation of beautiful chance discoveries. It must instead provide a systematic method for solving problems.
True and oft-heard though this story is, it is also easily taken for granted. Harvey Flaumenhaft’s new book Insights and Manipulations seeks to remedy that with a hands-on guide to this momentous change. To understand that change, he says, and to understand it as progress, “we need to know what it was a step from as well as what it was a step toward.” He presents it as a movement from the Conics of Apollonius of Perga, a brilliant and difficult triumph of ancient mathematics written in the third century b.c., to Descartes’s 1637 Geometry, a decisive stride into modernity. For Apollonius, mathematics was a way of gaining insights into the nature of geometrical forms by envisioning them in the mind; Descartes made mathematics into an activity of manipulation — hence the title of Flaumenhaft’s book.
But appreciating scientific progress should not become a license to forget the past:
We often take for granted the terms, the premises, and the methods that prevail in our time and place. We take for granted, as the starting points for our own thinking, the outcomes of a process of thinking by our predecessors.
What happens is something like this: Questions are asked, and answers are given. These answers in turn provoke new questions, with their own answers. The new questions are built from the answers that were given to the old questions, but the old questions are now no longer asked. Foundations get covered over by what is built upon them.
Progress thus can lead to a kind of forgetfulness, making us less thoughtful in some ways than the people whom we go beyond. We can become more thoughtful, though, by attending to the originating thinking that while out of sight is still at work in the achievements it has generated.
Insights and Manipulations is thus a guidebook helping us to retrace the steps of discovery from ancient mathematics to Descartes, who conceived the world anew. For “only by actively taking part in scientific discovery — only through engaging in re-discovery ourselves — can we avoid both blind reaction against the scientific enterprise and blind submission to it.” What’s at stake for Flaumenhaft is more than being thoughtful about the world we inhabit; it is whether we are to understand the foundations of modern science well enough to sustain it.
Classic works of science and mathematics make up a substantial part of the liberal arts curriculum at St. John’s College in Annapolis, Maryland, where Flaumenhaft has taught for more than fifty years. Students there struggle through Apollonius and Descartes not as an antiquarian exercise but as a way to see the modern world come into being.
Insights and Manipulations also offers a model of how to read a scientific classic: Presume that it has been written with care and treat it, like any other work of art, as a unified whole whose very form helps to tell its story. (Flaumenhaft provides, at times, more about the detailed structure of these works than many readers may want to know, but that’s a quibble.)
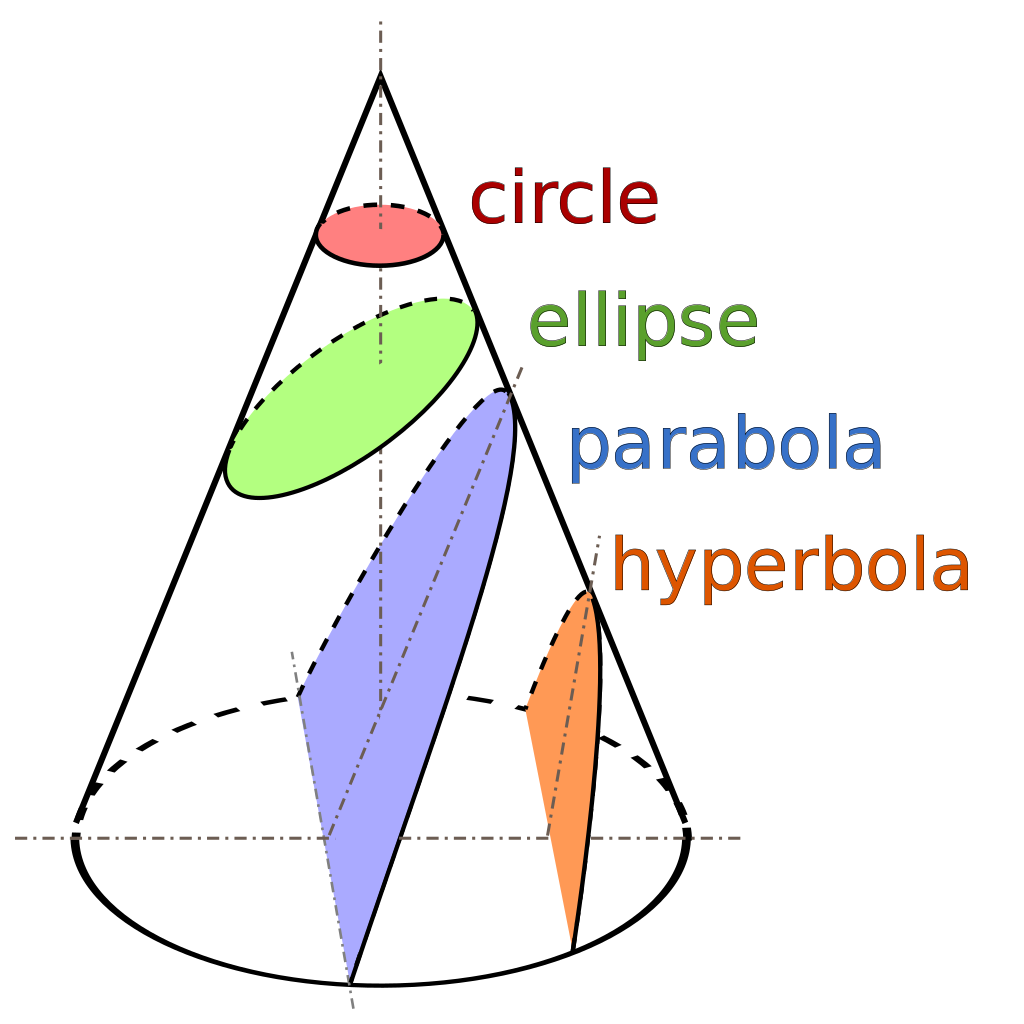
The first three-quarters of this hefty book is devoted to Apollonius, and is a considerable pedagogical achievement in itself. Apollonius studies conic sections, the curves obtained by slicing straight through a cone — circle, ellipse, parabola, hyperbola. The Conics is, to say the least, austere, a sequence of definitions, propositions, and proofs with little motivating explanation. It also assumes knowledge of sophisticated parts of Euclid’s Elements, a classical masterwork of geometry that preceded Apollonius by roughly a century.
Flaumenhaft, supplying background from Euclid as needed, carefully explains what each definition and proposition says (and, equally important, what it doesn’t). Before offering a formal proof, he prepares readers by informally explaining why each proposition ought to be true. He supplies abundant illustrations, not just geometric diagrams but also flowcharts that offer an overview of how every part of an argument fits together. The diagrams are great improvements on those typically provided in other presentations of Euclid or Apollonius. Instead of a single, sometimes massively complex figure, he accompanies each proof with a series of simpler pictures, each of which isolates only what is needed to explicate a single logical step. He also provides views from different angles (bird’s eye, side view), allowing the reader to imagine walking around a 3-D model. These illustrations are hand-drawn, which lends them a certain charm, as if one is following a teacher at a blackboard.
The story frequently steps back from the local questions of understanding individual definitions and arguments to the global question of why the results have been organized and presented as they are. Flaumenhaft tends, at times, to over-explain — as Marian Adams said of Henry James, to chew a bit more than he bit off — but that’s the defect of a virtue.
Conic sections still appear in high school mathematics today, but a contemporary student will encounter nothing like what we find in Apollonius. Apollonius starts with a geometrical image, a slice through a cone. Everything that follows is expressed in terms of geometrical constructions built on the cone, the curve, and the plane making the slice; there are no coordinates, formulas, equations, or even numbers. By contrast, a modern textbook will, pro forma, provide a picture of a cone, but will have no real use for it. The curves to be studied are defined by formulas, and the terminology of “conic sections” is a vestige of forgotten technology, as when we speak of dialing a phone. The modern student is really doing algebra.
Apollonius thinks very differently, guided by a set of clear logical distinctions that made it impossible to mix geometry with arithmetic (and thus with algebra). One must appreciate these distinctions to understand the radical step Descartes took in breaking them down, the power he unleashed in doing so, and the intellect that could do that.
After the extended treatment of Apollonius, and brief excursions into works by Diophantus of Alexandria (200s a.d.) and François Viète (1500s), Insights and Manipulations concludes with the 1637 Geometry. Here Descartes accuses the ancients of withholding explanations of how they discovered their results in order to make themselves look good. Further, the ancients insisted on a fundamental logical distinction between arithmetic and geometry — to Descartes, a pesky scruple that prevented them from finding the proper mathematical method. By merging the two fields, Descartes unveiled a royal road to discovery — inaugurating, as Flaumenhaft puts it, a decisive shift from seeing “with the mind’s eye” to performing “mental manipulation.”
Descartes famously distinguished mind, whose essence is to think, from matter, whose essence is “extension” — roughly, the ability to occupy space. The physics of the material world must therefore be explained as matter moving and rearranging in space. So a systematic method for solving geometrical problems, for mentally manipulating space, must have seemed the key to a comprehensive explanation of the material world.
Geometry was published in a volume comprising four short works. The first is the famous Discourse on the Method of Rightly Conducting One’s Reason and Seeking Truth in the Sciences — the source of “I think, therefore I am.” The other three offer examples of applying his method, which we can’t retrace here, to problems in different fields of science. Optics works out a (correct) law for the refraction of light. Meteorology explains (again correctly) the cause of a rainbow. Those two achievements, he says, are persuasive evidence for the value of his method.
And Descartes presents Geometry, the concluding essay, as definitive proof. He first describes a procedure for solving any problem in classical, Euclid-style geometry. A problem asks for a construction, such as: Given a rectangle, construct a square with the same area. I’ll use this very simple problem as a running example. Descartes doesn’t deign to illustrate his procedure by applying it to a specific example. Readers will learn more, he says, by working things out for themselves.
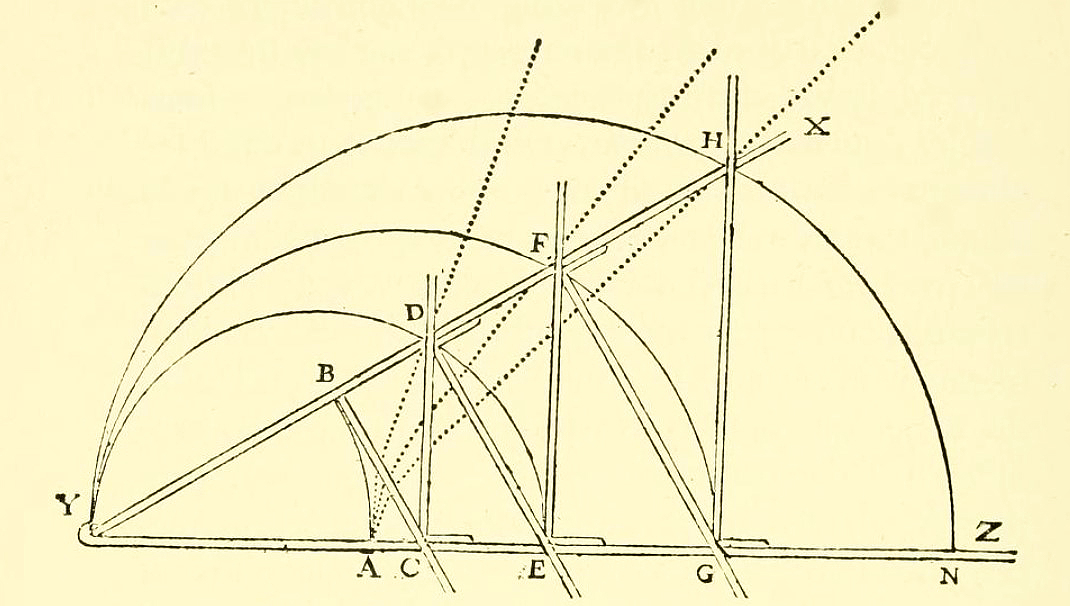
Instead, he turns to a problem that had been open for more than a millennium — actually to a family of problems called “locus” problems. They were formulated by Pappus of Alexandria, the last of the great, ancient Greek mathematicians, in the fourth century a.d. A locus problem asks a question of the form: What is the curve containing all points that satisfy some constraint? To take a simple example, if the constraint is “All points that lie at a given distance from a fixed center point,” the answer is a circle. Pappus formulated his problem in a very general way by establishing a systematic, stylized way to express the constraints. (See Supplement 1 below for an illustration.) While the answers to some relatively simple locus problems are the conic sections of Apollonius, the general problem posed by Pappus — an infinite family of increasingly complex problems — remained open.
Descartes is interested not merely in providing the answer to this or that previously unsolved problem, the stuff of which reputations in mathematics had always been made. What matters is the discovery of a systematic method for problem-solving — a way to attack any of Pappus’s locus problems, however elaborate the constraints. By doing so, he says, “I think I have entirely satisfied what Pappus tells us had been sought in this by the ancients,” and he adds, cavalierly, “I shall try to put the demonstration of it in a few words, for I am already bored from writing about it so much.”
The conceptual tools available for performing constructions in classical geometry are the straight edge and the compass. Although we may use physical versions of them on a blackboard, we should think of them as theoretical devices, imaginative ways to express two of Euclid’s postulates: that we can construct a straight line connecting any two points and extend it as far as we like (straight edge); and that we can construct a circle with any given center and radius (compass). Descartes’s methods allow him to see how far it’s possible to go using only straight edge and compass, and to identify the fancier tools required to solve more complex problems. He introduces what’s come to be called a “geometrical compass,” an indefinitely extendable device that allows additional moving straight-edges that act like levers:
As one adds more levers, one can draw more complex curves, with each added lever corresponding to added complexity in the algebraic expressions needed to formulate a problem.
Flaumenhaft writes:
When Descartes made his new beginning … , he said that the ancients were handicapped by their having a scruple against using the terms of arithmetic in geometry…. Before modern readers can appreciate why Descartes wanted to overcome the scruple, and what he saw that enabled him to do it, they must be clear about just what the scruple was.
We may think about the ancient scruple in the following way. The science we now have is what we might call “quantitative” and “numerical.” Quantities admit comparisons of less and greater. To us it seems natural to identify quantitative with numerical — to represent any quantity as a numerical value, for example a decimal number or a location on what we now call a “number line.” For that notion I’ll use the ungainly term number-in-our-sense.
To our great ancestors this conception of quantity, far from being natural, would have seemed incoherent. They recognized a fundamental difference between quantities arising in geometry (lengths, areas, volumes) and quantities arising in arithmetic (the numbers we count with). Our physical science required that Descartes break down that barrier by introducing arithmetical methods into geometry.
What was the problem? First, as noted, quantities fall naturally into two radically different categories: multitudes (collections of distinct individuals that can be counted, like cows) and magnitudes (which can be made continuously smaller or greater, like lines or areas or volumes). Ordinary speech reflects the difference. Of multitudes we ask “How many?” but of magnitudes “How much?” A herd of cows is a multitude; we ask how many cows are in a field, not how much cows there are. We get the answer by counting them. The water in a pond is a magnitude. We ask how much of it there is, not how many.
To define a multitude, we have to specify which individuals it consists of. One can’t point to a field and ask “How many?” without specifying how many of what: horses, cows, hooves. Euclid’s Elements, which lays the foundation for Apollonius, says that “a unit is that by virtue of which each of the things that exist is called one.” In this sense, “cow” is a unit but “water” is not; we can count cows but not water because there’s such a thing as “a cow” but no such thing as “a water.” There is an unfortunate collision between Euclid’s meaning of “unit” and our use of “unit” to denote some arbitrarily chosen magnitude — inch, pound, gallon — employed as a reference for measurements. It seems we might be able to paper over the differences between multitudes and magnitudes by using such reference values: We can’t ask how many water are in a pond, but we can ask how many gallons of water are in it. As we will see, that simple strategy — changing the question so as to think of magnitudes as multitudes — can’t be made to work. Something much deeper will be required.
Euclid goes on to say, “A number is a multitude composed of units.” Euclid’s units are, by definition, indivisible, so multitudes are discrete: There is no multitude consisting of more than three cows but fewer than four. Multitudes defined by different units can be compared: It makes sense to ask whether there are more chickens in the barn than eggs. From now on, I’ll use the word number, unqualified, to mean a number in this ancient sense but will sometimes, for emphasis, say “counting number,” and we will see how this is different from number-in-our-sense, which allows us to represent any quantity as a numerical value.
Magnitudes, by contrast, are not discrete; a line, unlike a herd of cows, can repeatedly be divided into smaller pieces as often as you like. (For Euclid, “line” always means what today we would prefer to call a “line segment”: limited in length, having two end points.) Equally important, magnitudes are of different kinds, and those of different kinds are incomparable; we can’t, for example, ask whether (the length of) a line is greater or less than (the area of) a two-dimensional figure such as a square.
The preceding sentence hid the references to length and area in parentheses because they suggest a way of thought according to which there is, on the one hand, a line (or a figure) and, on the other hand, some sort of number-in-our-sense that is its length (or its area). But the possibility or intelligibility of such numbers-in-our-sense is precisely what is at issue. When, for example, Euclid shows that a certain square equals a certain triangle, that amounts not to some numerical comparison but to showing that the figures can be cut into identical collections of pieces — or, if you like, cut up and then rearranged to make the same figures.
Consider a further distinction between multitudes (“how many”) and magnitudes (“how much”): Different things can be done with each. For example, two multitudes can be multiplied but two magnitudes cannot. The result of multiplying four cows by three is (to use a modern notation that is in this case not misleading) 4 + 4 + 4 cows. The multitudinous-ness of three is what tells us how many times to add groups of four cows together. By contrast, although we can multiply a magnitude by a multitude — say, doubling a line — we cannot multiply two magnitudes, even if they are of the same kind. We can’t multiply a line by a line or one figure by another, because lines and figures provide no natural answer to the question “How many times?”
A modern text that formulates the Pythagorean Theorem by saying “a right triangle with sides a, b, and hypotenuse c satisfies a2 + b2 = c2” is therefore saying something radically different from what Euclid or Apollonius or Pythagoras said. It assigns to the sides the lengths a, b, and c, which are numbers-in-our-sense; it performs arithmetical operations on them (squaring, adding) to compute other numbers-in-our-sense; and then it asserts that the results are numerically equal. Euclid puts this very differently. He says that if you’re given a right triangle and construct squares on all its sides, then the squares on the two sides containing the right angle taken together are equal to the square on the other one. Numbers don’t enter the picture, and the proof is done geometrically.
We are so used to thinking in terms of numbers-in-our-sense that the difference can be hard to think about, but it is critical for understanding what ancient mathematicians were doing, and what marked the divide between geometry and arithmetic that Descartes broke down. But before we get there, we must get a taste for the challenges the ancients faced — and the insights they gained — in doing geometry without arithmetic.
Earlier, I dismissed a maneuver that seems as if it could bridge the two domains — namely, to treat a magnitude as a kind of multitude, an exact multiple of some magnitude used as the reference for a measurement. Thus we might be able to regard some line as a multitude of feet or meters or cubits. If a right triangle has sides that are 3 feet, 4 feet, and 5 feet, the Pythagorean Theorem might be expressed as a fact about calculations with those numbers: 32 + 42 = 52. (Ignore for now that the theorem would no longer describe visualizable relationships among geometric figures.)
Why does this trick fail? It can be applied only if all the lines in the problem are exact multiples of the same reference line — if, in Euclid’s terminology, all the lines have a “common measure.” Unfortunately, one of the most famous proofs in ancient mathematics shows that that’s not always possible. A simple example: the side of a square and its diagonal have no common measure. This example also shows that the trick can’t be used to formulate the Pythagorean Theorem. It can’t be applied to the right triangles that result from slicing a square in half along its diagonal.
Ancient mathematicians devised an elegant way around this by appealing to the notion of ratio. Quantities of the same kind — two lines, for example — will have a ratio even if they lack a common measure, and ratios can be compared. We can say, for example, that the ratio of 2 to 5 is the same as the ratio of 4 to 10, and is greater than the ratio of 2 to 10. Crucially, we can compare any ratios — we can, for example, compare the ratio of two counting numbers to that of two areas, or the ratio of two lengths to the ratio of two volumes.
Modern mathematics is indifferent to any distinction between ratios and numbers-in-our-sense; it is happy to identify the ratio of 2 to 5 with the number-in-our-sense 2/5, or the ratio between a square’s diagonal and its side with the number-in-our-sense called “the square root of two.” For us, the proportion stating that “the ratio of 2 to 5 is the same as the ratio of 4 to 10” can be expressed as the equation “2/5 = 4/10.”
Euclid and Apollonius have no words to denote “the square root of two” but do have a powerful theory of ratios that makes it possible to establish connections among quantities of all kinds. That theory gets a rigorous basis in the most technically sophisticated book of Euclid’s Elements.
Consider a simple example, expressing the relation between the area of a rectangle and the lengths of its sides. In modern mathematics we represent the sides with numbers-in-our-sense — say, 2.6 and 3.5 — and define the area to be their numerical product: 2.6 * 3.5 = 9.1. In a practical application, the numbers we use will depend on whether we choose to express the lengths in inches, meters, furlongs, or whatever.
Euclid expresses that relationship more elegantly with ratios, needing no resort to an arbitrarily chosen standard of measurement. Look first at a simple case. If, given a rectangle, we leave its height unchanged, and double its width, we will have doubled its area. Similarly, to use modern terms, if we change the width by a factor of 50 percent, or by a factor of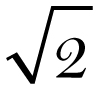 
, we will change the area by the same factor. That is, if we write “:” to abbreviate “the ratio” between two quantities, we can in this simple case express the relation between the sides and area of a rectangle as a proportion:
[old rectangle : new rectangle] is the same as [old width : new width]
If we now change both the height and width, then [old rectangle : new rectangle] will be a ratio that depends on both [old width : new width] and [old height : new height]. It will be what Euclid calls the ratio compounded of those two; given such a pair, Euclid shows how to construct a pair of lines whose ratio is their compound.
These are the terms in which Apollonius thinks, and he deploys them with great virtuosity.
Flaumenhaft wants to help us teach ourselves to think like Apollonius, who proves theorems using proportions, and to compare that to the Cartesian practice of solving problems using equations. The root of the Greek word for “theorem” means “to look at” or “behold.” And “proportion” has to do with recognizing a similarity between different things. This reflects what Apollonius does: behold certain similarities in things. A problem, by contrast, presents us with a task: to find a solution. The terms in an equation are symbolic. Their purpose is not to represent something that we see by looking at or through it, but to be material for manipulation.
For Descartes, Flaumenhaft writes, “beholding is subordinate to mastery,” and “wonder should give way to problem-solving. What Descartes brought to this modern project which took mastery of nature as its end was an emphasis on mathematics as means to the end.”
We can further contrast the two approaches by considering the difference between synthesis and analysis. Euclid and Apollonius present their results by synthesis. A synthesis is a proof that begins from postulates and things already proven, then deduces a sequence of further results until it manages to establish the desired conclusion. Those deductions often concern not only the lines and figures given in the statement of a theorem, but additional lines and figures introduced, often with great ingenuity, in order to establish in some roundabout way relationships among the elements of the original material. How the proposition or its proof were discovered is not manifest.
Descartes, by contrast, provides a method of analysis. Starting with a problem, he will transform it into a sequence of other problems, all of which are equivalent, until arriving at one he knows how to solve. Since the problems are equivalent, a solution to any of them gives a solution to all of them. The procedure is transparent because the analysis itself shows how the result was obtained.
Analysis is what we do in a high school algebra class. We’re given the problem of finding an x such that 3x – 2 = 7. Adding 2 on each side of the equation transforms it to 3x = 9. Dividing both sides by 3 transforms that to x = 3. Maneuvers of this kind were hardly unknown before Descartes. Flaumenhaft walks us through the way Diophantus applied them to problems about numbers and Viète applied them to what he called “species” — entities that share some characteristics with numbers and some with geometrical magnitudes. Species, however, are still encumbered by something like the distinctions among kinds of quantities that Descartes eliminates.
Descartes claims that any geometric problem can be expressed as the task of finding the lengths of certain lines. To do that by analysis, he first restates the geometric problem using equations that relate the unknowns (lines to be found) to the knowns (lines given in the statement of the problem).
Consider again our familiar example: Given a rectangle, construct a square of the same area. The knowns are the two sides of the rectangle; call them A and B. There’s one unknown, the side of the square we’re looking for (since all sides of the square are the same); call it x.
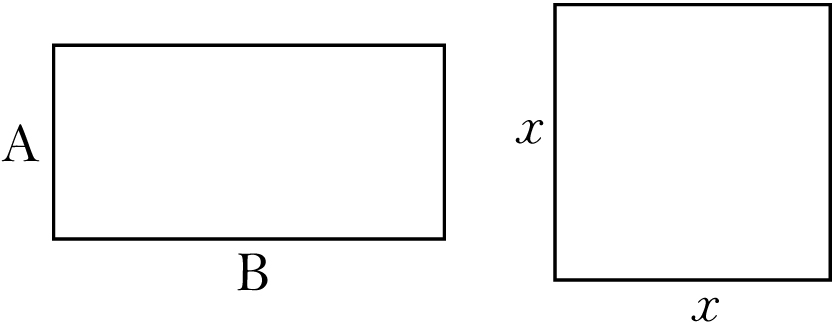
The equation that relates the areas of the two figures may look misleadingly, comfortably familiar:
x * x = A * B
We’ll have more to say about that later, but, to avoid jumping to unjustified conclusions, note that Descartes is doing geometry: A, B, and x are straight lines, not numbers.
Algebraic manipulations then transform these equations into a solution — that is, a collection of equations in which each unknown is set equal to an expression involving only known quantities.
In this case, the solution (also misleadingly familiar) is:
Now comes a piece of magic. Descartes does not find x by calculating some value for the expression 
; instead, as we will see below,“” is interpreted as a set of instructions for performing a geometrical construction that gives the desired answer.
He is doing geometry, but the most important steps take place in a symbolic world where we (literally) lose sight of the original subject matter. We can, however, extract a geometrical meaning from the symbolic solution that emerges.
Before looking at how Descartes solves the problem, we must consider how he explains arithmetical manipulation of lines. The terms in Descartes’s equations use the operations of addition, subtraction, multiplication, division, and the taking of roots (square root, cube root, and so forth). As Descartes defines these operations, both their inputs and outputs are lines. Thus, all the manipulations act on a single kind of thing — on a single “type,” to use the terminology of modern logic and computer science. Operating on a single type, regardless of what it represents, is a crucial simplification.
Addition and subtraction of lines are explained in the obvious way: A + B is a line that results from extending A by attaching B at one of its endpoints. A – B is a line that results from lopping B off the end of A, and is not defined if B is greater than A. Descartes defines multiplication, division, and the taking of roots by analogy. Take multiplication as an example. He first finds a recipe that characterizes multiplication for counting numbers in terms of ratios and proportions — the domain in which multitudes and magnitudes participate on something like an equal footing. He then uses that recipe as the definition of multiplication for lines.
Here’s how that works. For counting numbers, we can describe the result of multiplying 2 by 3 as a proportion by saying that
(2 * 3) : 2 is the same ratio as 3 : 1
In other words, because 3 is what you get by tripling 1, the value of 2 * 3 is what you get by tripling 2. Descartes simply copies that: If A and B are lines and we arbitrarily choose any other line u, then — in terms of that choice of u — we define A * B to be a line such that
(A * B) : A is the same ratio as B : u
That is, whatever “multiple” B is of u, A * B is that same multiple of A. (Supplement 2 below provides a geometrical construction for finding A * B.) Descartes calls u a “unit,” using the word in essentially the modern sense — unlike Euclid’s usage, in which a unit is a concept that specifies the kind of thing (a cow) assembled in a multitude (a herd).
It’s far from obvious what those definitions buy us, since the line we obtain by calculating the value of some complex expression will depend entirely on the arbitrarily chosen unit (u). But Descartes doesn’t want to calculate with these expressions; he only wants to manipulate them. His strategy works, because, for any fixed choice of a unit, all the usual rules for algebraic manipulation are valid. For example, consider the expressions (A * B * C) / A and B * C. Whatever line we choose as the unit u, the value of the two expressions calculated in terms of u will be lines of the same length. Descartes can therefore say that (A * B * C) / A = B * C, and justify the algebraic maneuver of “canceling the A’s.”
Here are the steps by which Descartes’s method would solve our simple sample problem: Given a rectangle, construct an equal square.
We choose names for the knowns, the sides of the rectangle: call them A and B. We choose a name, x, for the side of the square we’re seeking.
We next apply certain rules for translating the geometry into symbols. One of them tells us to represent (the area of) that rectangle by the expression A * B. By the same rule, x * x represents the square we want to find. (For x * x, we’ll use the modern notation x2, which Descartes introduced.) We thus reformulate the problem as a request to solve x2 = A * B. A symbolic solution requires just two steps:
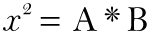 | the problem |
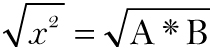 | taking the square root of both sides |
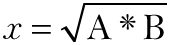| since  |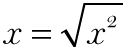
Descartes provides another set of rules for translating the solution thus found into a geometric construction. Relegating the explanation to Supplement 3 below, I’ll simply assert that the solution given above corresponds to a geometric construction solving the problem:
Find an x so that B : x is the same as x : A.
All together, this amounts to a geometrical argument in which all the work is done by routine symbolic manipulation.
The rules for translating geometric problems into equations, and for then translating their algebraic solutions back into geometric constructions, are based on plausible analogies. Further, because the rules for algebraic manipulation are valid regardless of the choice of unit, it’s plausible that those manipulations won’t corrupt the geometrical meaning that we ultimately wish to extract. Those deep insights don’t truly amount to proof that his method works, although using modern logical techniques such a proof would be straightforward.
Descartes asserts, leaving it to the reader to persuade himself, that the method he describes suffices to solve any problem solvable by the constructions available in Euclid. But that’s only a warmup.
The definitive proof for the value of Descartes’s method is that it has enabled him to discover how to systematically classify and solve an unlimited number of problems of arbitrary complexity. Locus problems with more and more elaborate constraints will result in equations containing terms of higher and higher power, something that might in the past have seemed problematic. We can understand X2 — indeed, visualize it — as representing the area of a square, and we can understand X3 as the volume of a cube. But what about X4, X5, X6, … ? What could be the sense of those? Descartes has made that problem disappear. There is a method. One applies it.
He thus helped set in motion a chain of developments that led mathematics to become formal. Euclid and Apollonius understand themselves to be talking about lines, circles, figures, and solids. They single out certain obvious truths as postulates and prove others, including some that are not at all obvious, from those postulates. Those proofs allow us to see that the less-obvious things are true, but don’t make them true; rather, their truth follows from the nature of lines, circles, figures, and solids.
A modern treatment of Euclidean geometry, by contrast, might begin by saying something like this: Suppose we have two collections of things, which we choose to call points and lines, and suppose that they satisfy such-and-such a list of postulates. It doesn’t matter, and we don’t care, what the things called “lines” and “points” are in relation to space or to anything in the physical world; the question doesn’t arise. Such meaning as “lines” and “points” have is acquired from the role they play in the system. Bertrand Russell, with his talent for aphorism, expressed this by saying that “mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.”
Practicing mathematicians do of course form mental pictures of what they talk about. Few have carefully thought-through positions on the philosophical status of those entities, but, professionally speaking, all play the formal game because it has immense power — and is the only way to make their results acceptable to the mathematical community at large.
Insights and Manipulations is written, the introduction says, “for serious amateurs by a serious amateur,” and even its smallest details reflect the author’s long career as a teacher. Its meticulous layout, for example, arranges that an illustration and any references to it will lie on the same page or on a facing page, so that the reader won’t be compelled to flip back and forth. The original texts, including Flaumenhaft’s new translation of Apollonius, are presented in gray boxes and arranged to help the eye take them in, with lengthy and complex sentences often displayed so that each line on the page consists essentially of a logical unit. The publisher deserves compliments for agreeing to design decisions that make a big book even bigger.
A serious amateur could use this book for self-study with a good prospect of success. Small seminars, I’m told, have worked through the entirety of early drafts with university students. A profitable course could be made from selections that focus, like this essay, on the beginning and end of the story — Apollonius and Descartes.
Insights and Manipulations is part of a long-term pedagogical project, of the author and others, to reintroduce classic scientific works into liberal education. Intellectually serious students are owed that experience. Great scientific works are of enduring interest for their daring and imagination, and as chronicles of heroic adventures of the mind. “To be thoughtful human beings,” Flaumenhaft says, “to be thoughtful about what it is that makes us human, we need to read the record of the thinking that has shaped the world around us, and continues still to shape our minds.”
A simple three-line locus problem is illustrated below:
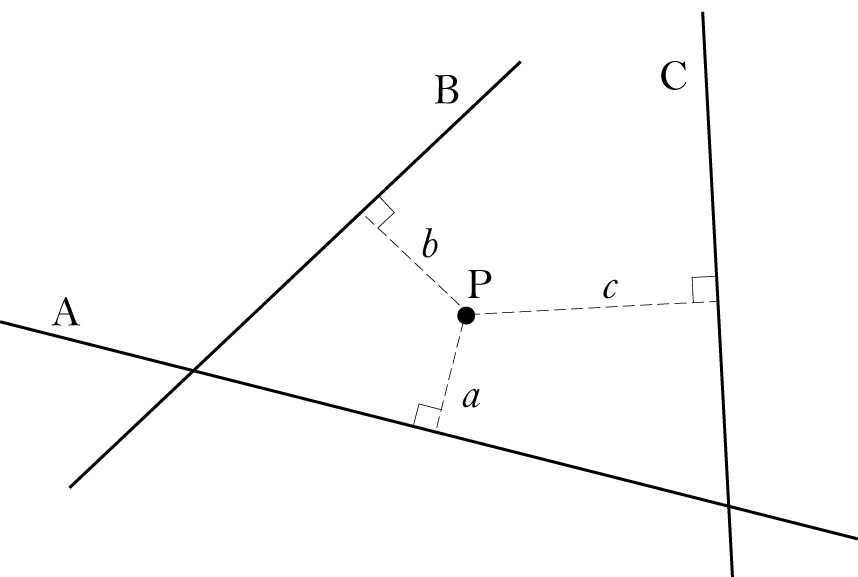
We’re given the “reference” lines A, B, and C. Here is the constraint
determining whether a point P lies on the locus:
Draw perpendiculars from P to each of the reference lines, calling
those perpendiculars a, b, and c. P satisfies the constraint if
you can draw a rectangle with sides a and b that has the same
area as a square with side c.
In this diagram, c is larger than both a and b. Thus we would expect the square with side c to be larger than the rectangle with sides a and b, and so P does not lie on the locus.
Pappus introduced a very general way to formulate constraints: There can be any number of reference lines, not just three. Instead of insisting that the line drawn from P meets each reference line at a right angle, one can specify the angle for each of them — the line from P to A must make this angle; the line from P to B must make that one; and so forth. Instead of requiring that the areas of the rectangle and square be equal, one can specify that the areas must have a certain ratio. (In, say, a six-line problem, the way to formulate the comparison of ratios based on the six lines drawn from P to the reference lines is more complex.)
Given A, B, and u, lay them out as in the left-hand side of the figure
below:
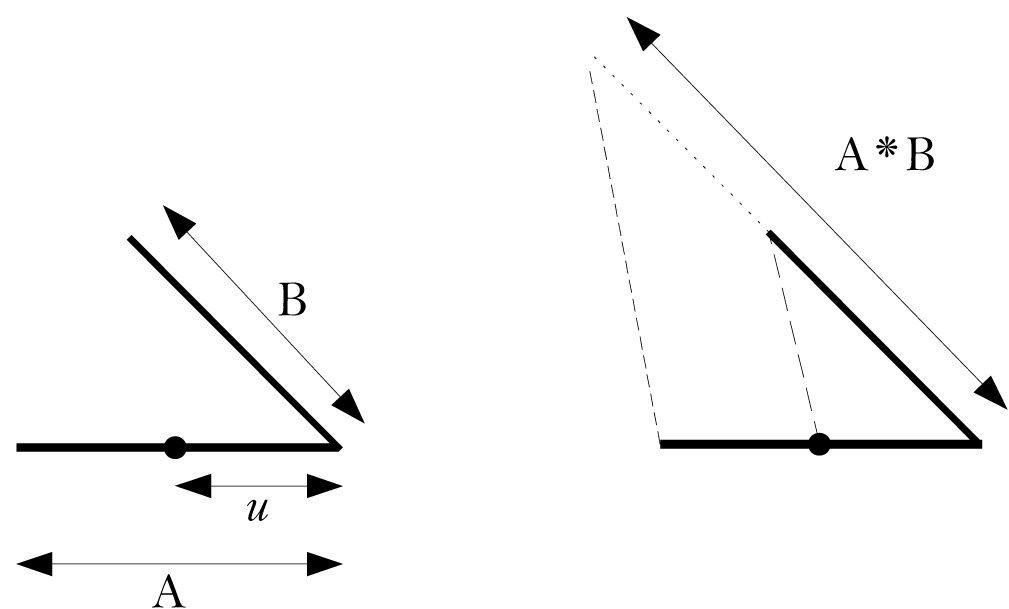
A and B meet at their end points to form an angle (it doesn’t matter what size). Lying on one of those sides is u (it doesn’t matter which side; in the figure I’ve chosen A), with one of its end points at the angle’s vertex. Neither does it matter whether u is greater than, less than, or equal to the side on which it lies.
The right-hand side of the figure then shows how to construct the side that will be defined as the length A * B with respect to the unit u: Draw a line (shown with heavy dashes) from the end of u to the end of B. Then draw a line (shown with lighter dashes) parallel to that line at the end of A, extending that line, and adding an extension to B, until they meet.
The desired result is the line marked A * B. Because the two dashed lines are parallel, the two triangles in the figure are similar, and corresponding sides will therefore have the same ratio. So, as desired, (A * B) : A is the same as B : u.
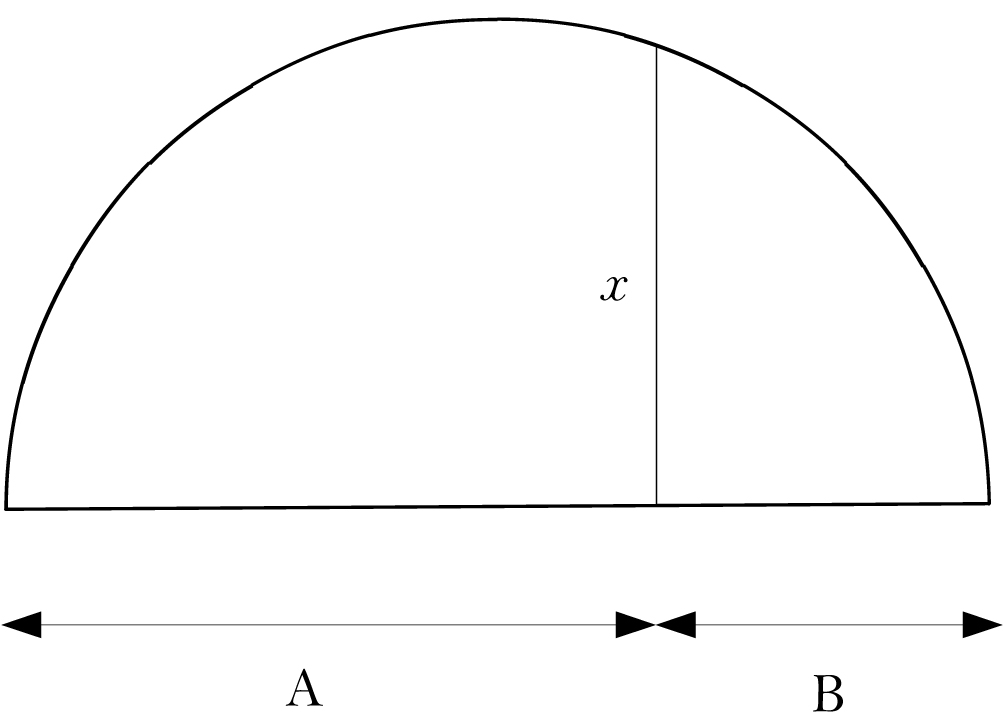
Let’s first explain why this equation corresponds to the proportion:
B : x is the same as x : A
This can be seen by backing up to the preceding equation, x2 = A * B, and rewriting it as follows:
| x * x = A * B | by the definition of x2 |
| x = (A * B) / x | dividing both sides by x |
| x / A = (A * B) / (x * A) | dividing both sides by A |
| x / A = B / x | “canceling” the A’s |
This last equation corresponds to the proportion
B : x is the same as x : A
The figure below shows the construction of x from B and A. Draw a semicircle whose diameter is A + B. The line x is the perpendicular drawn from the common point of A and B to the circle. The ability to draw circles (a compass) makes it possible to construct square roots. Successive add-ons to Descartes’s improved compass make it possible to extract roots of higher powers.
Exhausted by science and tech debates that go nowhere?
