

Our “ancient instinct of astonishment,” suggests G.K. Chesterton, is awakened when we consider how the world could have been very different. The possibilities of existence are explored in fairy tales and fuel children’s endless questions about why the universe is the way it is. This kind of curiosity, if left unchecked in youth, can easily develop into a career in physics.
Physicists’ deepest theories of the cosmos have several loose ends. They leave open a set of possibilities — ways that our universe could have been. They describe our universe, but can just as easily describe universes that started differently, or that have different fundamental properties. If we want to know why the universe is as it is, we need to know why, of all the possibilities, ours is the actual universe. Just as science has illuminated our place in the solar system, the galaxy, and the universe at large, we must consider our place in the laws of nature.
Physicists tend to picture the advancement of science in two ways. The experimentalist dreams of new data that overthrows our current theories. For example, in 1905 Henri Poincaré called the element radium “that grand revolutionist of the present time,” a substance that glowed for months on end with no obvious energy source. Perhaps energy is not conserved, or perhaps atoms have an enormous internal reservoir of energy. Either way, something about physics had to change.
The theorist, on the other hand, seeks a creative insight that explains the world in a simpler, more elegant, more unified way. For example, when Apollo astronaut David Scott dropped a hammer and a feather on the Moon, they hit the ground at the same time. This was a dramatic illustration of the long-understood but still counterintuitive truth that weight does not determine how fast an object will fall. But it took the genius of Einstein, reasoning theoretically, to show that gravity is the curvature of space and time, and that this explains why the hammer and the feather fall together — the curvature of space and time caused by the mass of the moon is the same for both, and so both travel in the same locally straight paths along the curvature of spacetime.
Experimentalists are still studying complex phenomena like turbulence and superconductors, still making new observations with supercolliders and space telescopes and other tools, still finding all kinds of unexplained data for theorists to puzzle over. Underlying all of these endeavors, however, is a question that has vexed physicists ever since Thales first postulated that water was the unifying principle of the cosmos: What are the most fundamental laws and principles of nature?
Today, our deepest understanding of the laws of nature is summarized in a set of equations. Using these equations, we can make very precise calculations of the most elementary physical phenomena, calculations that are confirmed by experimental evidence. But to make these predictions, we have to plug in some numbers that cannot themselves be calculated but are derived from measurements of some of the most basic features of the physical universe. These numbers specify such crucial quantities as the masses of fundamental particles and the strengths of their mutual interactions. After extensive experiments under all manner of conditions, physicists have found that these numbers appear not to change in different times and places, so they are called the fundamental constants of nature.
These constants represent the edge of our knowledge. Richard Feynman called one of them — the fine-structure constant, which characterizes the amount of electromagnetic force between charged elementary particles like electrons — “one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man.” An innovative, elegant physical theory that actually predicts the values of these constants would be among the greatest achievements of twenty-first-century physics.
Many have tried and failed. The fine-structure constant, for example, is approximately equal to 1/137, a number that has inspired a lot of worthless numerology, even from some otherwise serious scientists. Most physicists have received unsolicited e-mails and manuscripts from over-excited hobbyists that proclaim, often in ALL CAPS and using high-school algebra, to have unlocked the mysteries of the universe by explaining the constants of nature.
Since physicists have not discovered a deep underlying reason for why these constants are what they are, we might well ask the seemingly simple question: What if they were different? What would happen in a hypothetical universe in which the fundamental constants of nature had other values?
There is nothing mathematically wrong with these hypothetical universes. But there is one thing that they almost always lack — life. Or, indeed, anything remotely resembling life. Or even the complexity upon which life relies to store information, gather nutrients, and reproduce. A universe that has just small tweaks in the fundamental constants might not have any of the chemical bonds that give us molecules, so say farewell to DNA, and also to rocks, water, and planets. Other tweaks could make the formation of stars or even atoms impossible. And with some values for the physical constants, the universe would have flickered out of existence in a fraction of a second. That the constants are all arranged in what is, mathematically speaking, the very improbable combination that makes our grand, complex, life-bearing universe possible is what physicists mean when they talk about the “fine-tuning” of the universe for life.
Let’s consider a few examples of the many and varied consequences of messing with the fundamental constants of nature, the initial conditions of the universe, and the mathematical form of the laws themselves.
You are made of cells; cells are made of molecules; molecules of atoms; and atoms of protons, neutrons, and electrons. Protons and neutrons, in turn, are made of quarks. We have not seen any evidence that electrons and quarks are made of anything more fundamental (though other fundamental particles, like the Higgs boson of recent fame, have also been discovered in addition to quarks and electrons). The results of all our investigations into the fundamental building blocks of matter and energy are summarized in the Standard Model of particle physics, which is essentially one long, imposing equation. Within this equation, there are twenty-six constants, describing the masses of the fifteen fundamental particles, along with values needed for calculating the forces between them, and a few others. We have measured the mass of an electron to be about 9.1 x 10-28 grams, which is really very small — if each electron in an apple weighed as much as a grain of sand, the apple would weigh more than Mount Everest. The other two fundamental constituents of atoms, the up and down quarks, are a bit bigger, coming in at 4.1 x 10-27 and 8.6 x 10-27 grams, respectively. These numbers, relative to each other and to the other constants of the Standard Model, are a mystery to physics. Like the fine-structure constant, we don’t know why they are what they are.
However, we can calculate all the ways the universe could be disastrously ill-suited for life if the masses of these particles were different. For example, if the down quark’s mass were 2.6 x 10-26 grams or more, then adios, periodic table! There would be just one chemical element and no chemical compounds, in stark contrast to the approximately 60 million known chemical compounds in our universe.
With even smaller adjustments to these masses, we can make universes in which the only stable element is hydrogen-like. Once again, kiss your chemistry textbook goodbye, as we would be left with one type of atom and one chemical reaction. If the up quark weighed 2.4 x 10-26 grams, things would be even worse — a universe of only neutrons, with no elements, no atoms, and no chemistry whatsoever.
The universe we happen to have is so surprising under the Standard Model because the fundamental particles of which atoms are composed are, in the words of cosmologist Leonard Susskind, “absurdly light.” Compared to the range of possible masses that the particles described by the Standard Model could have, the range that avoids these kinds of complexity-obliterating disasters is extremely small. Imagine a huge chalkboard, with each point on the board representing a possible value for the up and down quark masses. If we wanted to color the parts of the board that support the chemistry that underpins life, and have our handiwork visible to the human eye, the chalkboard would have to be about ten light years (a hundred trillion kilometers) high.
And that’s just for the masses of some of the fundamental particles. There are also the fundamental forces that account for the interactions between the particles. The strong nuclear force, for example, is the glue that holds protons and neutrons together in the nuclei of atoms. If, in a hypothetical universe, it is too weak, then nuclei are not stable and the periodic table disappears again. If it is too strong, then the intense heat of the early universe could convert all hydrogen into helium — meaning that there could be no water, and that 99.97 percent of the 24 million carbon compounds we have discovered would be impossible, too. And, as the chart to the right shows, the forces, like the masses, must be in the right balance. If the electromagnetic force, which is responsible for the attraction and repulsion of charged particles, is too strong or too weak compared to the strong nuclear force, anything from stars to chemical compounds would be impossible.
Stars are particularly finicky when it comes to fundamental constants. If the masses of the fundamental particles are not extremely small, then stars burn out very quickly. Stars in our universe also have the remarkable ability to produce both carbon and oxygen, two of the most important elements to biology. But, a change of just a few percent in the up and down quarks’ masses, or in the forces that hold atoms together, is enough to upset this ability — stars would make either carbon or oxygen, but not both.
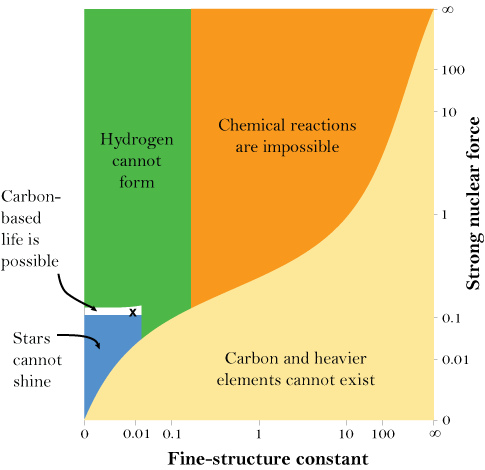
The numbers that characterize our universe as a whole similarly seem to be finely tuned. In 1998, astronomers discovered that there is a form of energy in our cosmos with the unusual property of “negative pressure” that operates something like a repulsive form of gravity, causing the universe’s expansion to accelerate. In the set of possible values for this “dark energy,” the vast majority either cause the universe to expand so rapidly that no structure could ever form, or else cause the universe to collapse back in on itself mere moments after coming into being.
The lack of an explanation for the fundamental constants in the Standard Model suggests that there is still work to be done. Particle physicist David Gross is fond of quoting Winston Churchill to his fellow scientists when it comes to explaining the seemingly arbitrary constants of nature in the Standard Model: “never, never, never give up!”
Perhaps someday, if the Standard Model is supplanted by a superior theory, physicists will not have to wonder about these constants because they will have been replaced by mathematical formulas derived from a deep law of nature. If — or when — physicists can confidently say why the constants of nature could not have been different, then it would no longer make any sense to speak of the consequences of changing their values, and so fine-tuning would be much less mysterious.
Then again, even a theory free of arbitrary constants would not necessarily explain why the universe gives rise to living beings like us. If these hoped-for deeper equations are anything like all the equations of physics thus far, then they, too, will still require initial conditions. The laws specify how the stuff of the universe behaves in a given scenario; they do not specify the scenario.
More fundamentally, the most that follows from a constant-free theory is this: if you want to consider different universes, you will need to consider different laws, not just different constants in the same laws. So, rather than talking about the fine-tuning of the constants, we would consider the fine-tuning of the symmetries and abstract principles. Could it be just a lucky coincidence that they produce in our universe the properties and interactions required by complex structures such as life? This notion “really strains credulity,” according to Frank Wilczek, who shared the 2004 Nobel Prize in Physics with David Gross. And as Bernard Carr and Martin Rees wrote in the conclusion of an influential early paper on the fine-tuning problem, “it would still be remarkable that the relationships dictated by physical theory happened also to be those propitious for life.”
Another approach to the fine-tuning problem comes from the discipline of cosmology, the study of the origins and structure of the universe. Some of the most important early modern science was cosmology, namely the work of Copernicus, Kepler, and Galileo to discover the structure of the solar system. In 1596, Kepler presented a beautiful mathematical theory to explain some important cosmic numbers: the distances to the six (known) planets. In his model, the planets were carried around on a set of nested celestial spheres, centered on the sun. Inside each sphere was one of the five Platonic solids — octahedron, icosahedron, dodecahedron, tetrahedron, and cube. Properly arranged, these six spheres separated by the five Platonic solids correctly spaced the planets, as far as anyone in the late sixteenth century could tell, and what’s more, it explained why there were only six planets.Alas, this beautiful hypothesis was slain by ugly facts: there are more than six planets in the solar system, and, in any case, the planets do not follow the circular orbits described by Kepler. This model was too simple, too idealized; the real solar system is molded in part by accident and contingency, having formed from a collapsing, turbulent disk of gas and dust surrounding the young sun. Facts about our solar system such as the distances between our sun and our planets, and the shape of their orbits, are local variables, not deep truths written into the laws of nature. They could have been different; in the thousands of other planetary systems we have observed in recent decades they are different.
So what if looking for the golden formula for such features of our universe as the fine-structure constant is as doomed as Kepler’s Platonic solar system? What if this “constant” is actually just a local, environmental variable, not something immutably written into the laws of nature? We have probed the fundamental constants using observations of the distant universe and found them unchanged. But of course we can only see so far, and in so much detail, with our telescopes. Wouldn’t it be surprising if none of our two dozen constants turned out to be variables?
Consider what this means for the fine-tuning question. If the “constants” actually vary from place to place and from time to time, then the right combination of constants for life is bound to turn up somewhere. And, of course, life can only exist in life-permitting regions. This kind of explanation has a parallel in the solar system: why does the Earth, the planet we live on, orbit the Sun within the narrow strip that allows its temperature to remain mostly around that needed for liquid water? Because there are plenty of planets and stars out there, and it is far more likely that living things would have evolved to ask these questions on planets with liquid water.
Other planets are one thing; other universes are quite another. Some of our theories of the very earliest states of our cosmos may imply that we live in a large, variegated “multiverse.” Further, some theories that extend the Standard Model show how the constants could be shuffled in the early universe. But the physics of the multiverse hypothesis is speculative, as is its extrapolation to the universe as a whole. And there is no hope of direct observations to verify these ideas and help turn them into mature scientific theories.
That said, particular multiverse hypotheses can be tested, at least to some extent. Consider this example as an analogy: Alice predicts that a certain factory will make ninety-nine red widgets and one blue widget. Bob predicts the reverse: ninety-nine blue and one red. A single packet arrives from the factory and they open it to find a red widget. While neither theory is decisively confirmed or refuted, the evidence clearly favors Alice. Now compare two multiverse theories: the first predicts that, out of a hundred universes that contain life, ninety-nine would also contain dark energy, while the second predicts that only one of the one hundred will contain dark energy. Our observation that our own universe contains dark energy favors the first theory. Though the only universe we can observe is a livable one, we can still test multiverse theories by asking whether our universe is typical of the life-permitting universes in the theory.
Is this science? On the one hand, multiverse hypotheses are physical theories that make predictions about our universe, namely, about the constants of nature. These constants are exactly where our current theories run out of ideas, so coming up with a theory that would predict them, even as a statistical ensemble, would be an impressive achievement. On the other hand, the main selling point for multiverse theory — all those other universes with different fundamental constants — will forever remain beyond observational confirmation. And even if we postulate a multiverse, we would still need a more fundamental theory to explain how all these universes are generated, which could raise all the same kinds of fine-tuning problems.
The apparent fine-tuning of the universe for life raises also a host of interesting philosophical issues. In other scientific fields, we can usually obtain more evidence — just run the experiment again, or keep looking for phenomena the theory predicts. But in cosmology, our telescopes can only see so far. Maybe desperate scientific questions call for desperate scientific measures.
In the last few decades, developments in the mathematical study of probability have given scientists new tools for testing physical theories. The older views of probability relied on what is called “frequentist” statistics. Under this orthodox view of statistics, the word “probability” means something like the actual frequency of an event in an experiment; saying that the probability that a coin will land on heads is 50 percent just means that if you flipped the coin 100 times, the frequency of heads would be about 50. The newer view of probability is called Bayesianism, for Thomas Bayes, the eighteenth-century theologian and mathematician whose long-neglected work forms the basis for Bayesian probability. Instead of looking at probability as the frequency of events in an experiment, Bayesians see probability in terms of degrees of plausibility. With Bayesian probability, we can compare how likely different theories are in the light of available evidence.
With the Bayesian toolbox in hand, we need not insist on a strict dividing line between responsible extrapolation and reckless speculation. If “successful” multiverse theories — those that correctly predict our fundamental constants — are a dime a dozen, then none will be particularly likely in light of our available evidence. Think of a detective investigating a dead body, a spotless crime scene, and a room full of suspects; without further evidence, the case will remain unsolved. Alternatively, if fundamental theories of space, time, and matter provide a mechanism for generating a variegated ensemble of universes that is simple and well-grounded in known physics, then the multiverse may find a place in science as a reasonable extrapolation of a well-tested theory. Or, just as importantly, it may be discarded, not as an untested speculation but as a scientific failure. Currently, no multiverse theory can claim to be tested to this extent.
Moreover, nothing in the Bayesian approach limits its application to propositions about the physical world. Probabilities are degrees of plausibility, and can in principle be applied wherever human curiosity leads. Even if precise calculations of numerical values are impossible, we can ask the right questions.
In thinking about these problems, our approach to probability matters. The fine-tuning of the universe for life invites us to imagine that our fortuitous cosmic environment is improbable. A random spin of the cosmic dials, it seems, would almost certainly result in a universe unable to create and sustain the complexity required by life. But if probabilities must be dictated by physical theories and are about physical events, as the frequentist believes, then we cannot say that our constants are improbable. We have no physical theory that stands above the constants, informing us that they are unlikely.
However, within the Bayesian approach, probabilities are not confined within physical theories. We can state that, for example, naturalism — the idea that physical things are all that fundamentally exist — gives us no reason to expect that any particular universe or set of laws or constants is more likely than any other, because there are no true facts about the universe that stand above the ultimate laws of nature. According to naturalism, there is no explanation of why this rather than some other final law, why any law at all, why a mathematical law; no explanation, to borrow the words of Stephen Hawking, of what “breathes fire into the equations and makes a universe for them to describe.” Like the uninformed detective in a large room of suspects, the probability of naturalism is at the mercy of every possible way that concrete reality could be.
So, what if one day the Ultimate Law of Nature is laid out before us, like a completed crossword puzzle? Whatever we think about that law will have to be deeper than physics, so to speak. We will be thinking about science — that is, we will be doing philosophy. Even if the only fact about what is beyond physics is that “there is nothing beyond physics,” we must remember that this is a statement about physics, not of physics.
Naturalism is not the only game in town when it comes to explaining why some law of nature might be the ultimate one. Its competitors include axiarchism, the view that moral value, such as the goodness of embodied, free, conscious moral agents like us, can explain the existence of one kind of universe rather than another; or, in the words of John Leslie, the theory’s chief proponent, it is “the theory that the world exists because it should.” Theism is another alternative, according to which God designed the universe and its fundamental laws and constants. These two views can trim the list of candidate explanations of the fundamental laws of nature, heavily favoring those possible universes that permit the existence of valuable life forms like us. By suggesting that fundamental physical principles are calibrated to make the existence of beings like us possible, investigations into fine-tuning seem to lend support to these kinds of theories. A full appraisal of their merits would also need to consider their relative simplicity, and other aspects of human existence, such as goodness, beauty, and suffering.
Are we special? This is not the kind of question that science usually asks, and for good reason — we don’t have a specialometer. And yet, certain observations do hold a special place in science. The faint static detected in 1964 by the antenna of Arno Penzias and Robert Wilson seemed unremarkable; all scientific instruments are plagued by noise. Only when this experiment came to the attention of Robert Dicke and his colleagues at Princeton University was it realized that they had discovered the cosmic microwave background, a relic of the early universe.
Facts can be special to a theory. That is, they can be special because of what we can infer from them. Fine-tuning shows that life could be extraordinarily special in this sense. Our universe’s ability to create and sustain life is rare indeed; a highly explainable but as yet unexplained fact. It could point the way to deeper physics, or beyond this universe, or even to principles beyond the ultimate laws of nature.
Exhausted by science and tech debates that go nowhere?